南京聚谱检测科技有限公司李亮先生在“微区分析”发表文章,论述Sr同位素研究相关的计算方法。转载如下。
本文相关内容比较硬核(晦涩),但很“实用”(基础),比如Ploeg et al., 2018, Nature Communications的论文就利用类似原理处理Os同位素并进行始新世极热事件的研究,审稿人就曾要求推导相关公式。
如果你是地球化学专业的学生,或者使用相关的地球化学数据,可以尝试在Excel中进行练习。
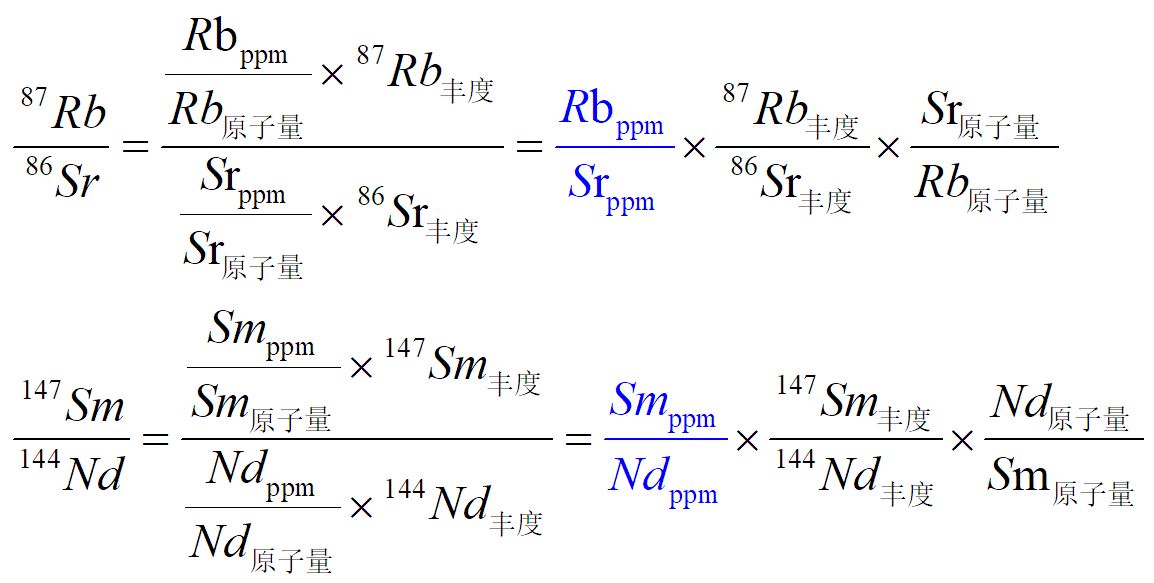
无论是做Rb-Sr定年(或Sm-Nd定年),还是做Sr-Nd同位素物源示踪,都需要知道87Rb/86Sr比值(或147Sm/144Nd比值)。
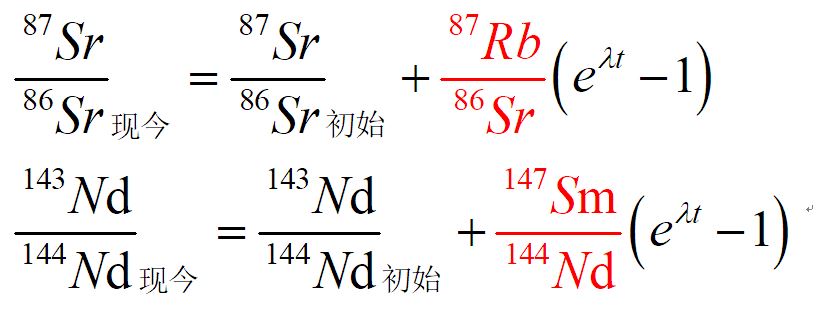
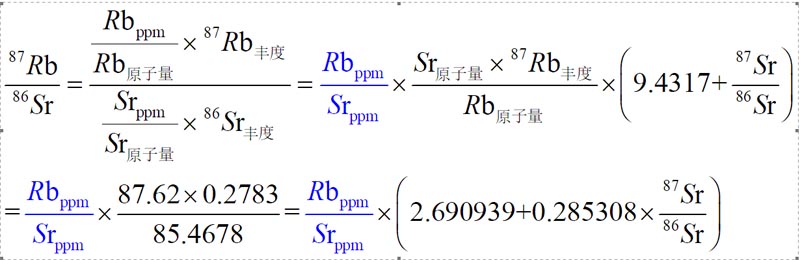
很多人以为这个比值是质谱仪测出来的,其实不然,这个比值是根据Rb, Sr ppm含量(或Sm, Nd ppm含量)计算得到的:
全岩粉末的Rb, Sr, Sm, Nd ppm含量,可引用ICP-MS微量元素测试值(通常不确定度较大),也可以通过同位素稀释质谱法(Isotope Dilution Mass Spectrometry = IDMS) 获得更加准确可靠的微量元素含量。
Rb, Sr, Sm, Nd的原子量和相应核素的自然丰度,可引用国际纯粹与应用化学联合会(IUPAC) 公布数值。
| 原子量 |
|
自然丰度 | ||
| Rb | 85.4678±3 |
|
87Rb | 0.2783±2 |
| Sr | 87.62±1 |
|
86Sr | 0.0986±1 |
| Nd | 144.242±3 |
|
144Nd | 0.23798±19 |
| Sm | 150.36±2 |
|
147Sm | 0.1499±18 |
87Rb通过β- 衰变为87Sr,半衰期488亿年。如果进一步考虑,在某个岩石(或矿物)内部,放射性成因87Sr*、143Nd*的丰寡会不会影响该体系内部87Sr与86Sr、143Nd与144Nd相对丰度,进而影响该体系的Sr、Nd原子量? 下面我们以Sr同位素为例,来进行讨论。锶Sr同位素原子量及相对比值如下,因为87Sr为放射性成因的,因此其相对86Sr的比值不确定,表示为x。
84Sr 83.91343 amu 84/86 Sr =0.0565
86Sr 85.90927 amu 86/86 Sr =1
87Sr 86.90889 amu 87/86 Sr = 变量x
88Sr 87.90562 amu 88/86 Sr =1/0.1194=8.3752
Σ SUM = 9.4317+x
此时该体系中,各个Sr同位素的丰度= (8X/86Sr)÷(Σ SUM)
例如86Sr 丰度= 1/ (9.4317 + 87/86Sr) Sr原子量= Σ (核素丰度×核素质量)
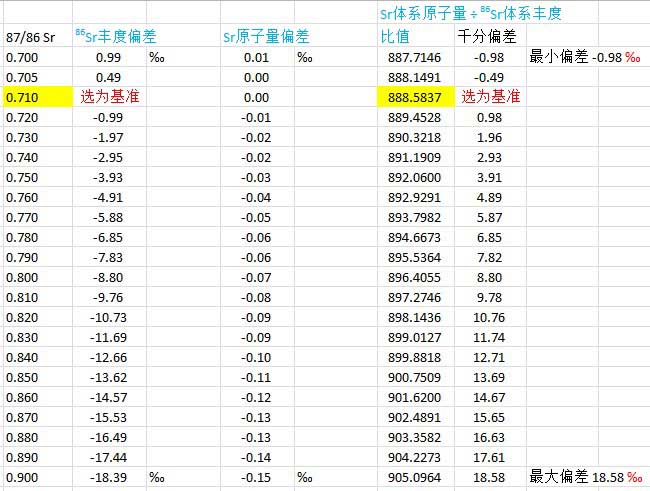
在常见的87/86Sr范围内( 0.700 ~ 0.900 ),计算如下:
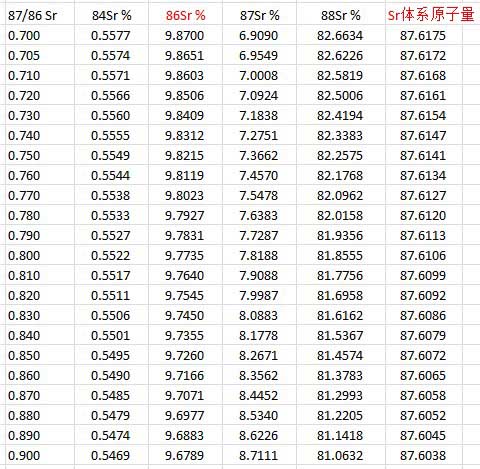
以0.710为基准(因为它的86Sr丰度最接近IUPAC数值0.0986±1)
某岩石(或矿物)体系内部:
(2.1) 86Sr丰度偏差 -18.39‰ 至+0.99‰;
(2.2) Sr原子量偏差 -0.15‰ 至+0.01‰;
(2.3) Sr原子量÷144Nd丰度,该比值偏差 -0.98‰至+18.58‰
计算该比值偏差 的近似公式 = [原子量偏差] 减去 [86Sr丰度偏差]
结论:相关体系87Rb/86Sr的计算公式应为: